Let ![]() denote the least common multiple. Prove that
denote the least common multiple. Prove that
![]()
for all ![]() .
.
Solution
For each ![]() of the form
of the form ![]() the number of solutions of
the number of solutions of ![]() is given by
is given by ![]() . It follows that the series is equal to
. It follows that the series is equal to
![Rendered by QuickLaTeX.com \[\sum_{M \geq 1} \frac{1}{M^s} \prod_{p \mid M} \left ( 2 \nu_p(M) + 1 \right )\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-1306b9ede00cc821b3dec2727a9ac1b3_l3.png)
and since the function ![]() is multiplicative we have successively:
is multiplicative we have successively:
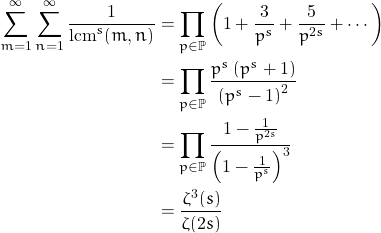
![Rendered by QuickLaTeX.com \[\lim_{n \rightarrow +\infty} \frac{1}{n^2} \sum_{k=1}^{n} \sigma(k) = \frac{\pi^2}{12}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-e50a8cb26cdfd69e44104e380a3b3a23_l3.png)
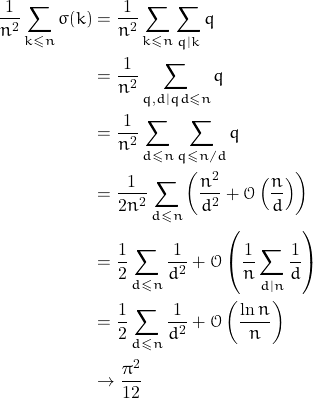
![Rendered by QuickLaTeX.com \[\lim_{N \rightarrow +\infty} \sum_{n=1}^{N} \frac{\left| \mu (n) \right|}{n} = +\infty\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-e170cf276a79dd717c4a88b3bc9ed237_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{N \rightarrow +\infty} \sum_{n=1}^{N} \frac{\left| \mu (n) \right|}{n} \geq \sum_{p \in \mathcal{P}} \frac{1}{p} = +\infty\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-869894447d42f294232b220f391ffdbb_l3.png)