Let ![]() . We define
. We define
![]()
It is known that this series converges. Prove that
![]()
Solution
We triangulise the matrix  , that is
, that is  where
where  is an invertible matrix and
is an invertible matrix and  is an upper triangular. This is possible since our matrix is over
is an upper triangular. This is possible since our matrix is over  and thus its characteristic polynomial splits. Let
and thus its characteristic polynomial splits. Let  be its eigenvalues. Then we note that
be its eigenvalues. Then we note that  is upper triangular with
is upper triangular with  in its diagonal. Hence
in its diagonal. Hence  is also upper triangular with
is also upper triangular with  in its diagonal. Hence
in its diagonal. Hence
![]()
However ![]() and
and ![]() forall
forall ![]() . Thus
. Thus ![]() and finally
and finally
![]()
The interested reader may also take a look at the exercise here at mathimatikoi.org .
Since the space of all
of all  complex matrices is a finite-dimensional vector space, all norms define the same topology. So we can take a sub-multiplicative norm, that is, a norm
complex matrices is a finite-dimensional vector space, all norms define the same topology. So we can take a sub-multiplicative norm, that is, a norm  such that
such that  . (For example, we can take
. (For example, we can take  to be the operator norm on E.) As a finite dimensional vector space, E is complete, so it’s enough to show normal convergence. We have that, for each integer
to be the operator norm on E.) As a finite dimensional vector space, E is complete, so it’s enough to show normal convergence. We have that, for each integer  ,
,
and we know that, for each real number , the series
, the series 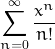 converges (it defines the exponential function). Therefore, for any
converges (it defines the exponential function). Therefore, for any  , the series
, the series 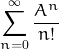 converges.
converges.
(We also got the additional result that . )
. )