Exponential matrix

Let $A \in \mathcal{M}_{n \times n} \left( \mathbb{C} \right)$ . We define

$e^A = \sum_{m=0}^{\infty} \frac{A^m}{m!}$

It is known that this series converges. Prove that

$\det (e^A) = e^{\Tr (A)}$

Solution

We triangulise the matrix $A$ , that is $A= P^{-1} T P$ where $P$ is an invertible matrix and $T$ is an upper triangular. This is possible since our matrix is over $\mathbb{C}$ and thus its characteristic polynomial splits. Let $\lambda_1, \lambda_2, \dots, \lambda_n$ be its eigenvalues. Then we note that $T^k$ is upper triangular with $\lambda_1^k , \lambda_2^k , \dots, \lambda_n^k$ in its diagonal. Hence $e^T$ is also upper triangular with $e^{\lambda_1}, e^{\lambda_2} , \dots, e^{\lambda_n}$ in its diagonal. Hence

$\det e^T=e^{\lambda_1} e^{\lambda_2} \cdots e^{\lambda_n}=e^{\lambda_1+\lambda_2 +\cdots+\lambda_n}=e^{\Tr (T)}$

However $\Tr (A) = \Tr (T)$ and $P^{-1} T^k P = A^k$ forall $k$ . Thus $P^{-1}e^TP=e^A$ and finally

$\det e^T=\det (P^{-1}e^TP)=\det e^A$

They might interest you:

Binomial sum

Uniform continuous

An inequality

Gamma infinite product

A rational harmonic series

Equality of fields

Series with cosine integral

Rational function and polynomial

Zero function

2 thoughts on “Exponential matrix”

The interested reader may also take a look at the exercise here at mathimatikoi.org .

Since the space $E:=\mathcal M_n(\mathbb C)$ of all $n \times n$ complex matrices is a finite-dimensional vector space, all norms define the same topology. So we can take a sub-multiplicative norm, that is, a norm $\lVert\cdot\rVert$ such that $\lVert AB\rVert\leq \lVert A\rVert \cdot\lVert B\rVert$ . (For example, we can take $\lVert\cdot\rVert$ to be the operator norm on E.) As a finite dimensional vector space, E is complete, so it’s enough to show normal convergence. We have that, for each integer $n \geq 0$ ,

$0\leq ||A^{n}/n!||\leq \frac{\lVert A\rVert^n}{n!}$

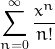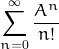and we know that, for each real number $x$ , the series $\displaystyle \sum_{n=0}^{\infty}\frac{x^n}{n!}$ converges (it defines the exponential function). Therefore, for any $A \in E$ , the series $\displaystyle \sum_{n=0}^{\infty}\frac{A^n}{n!}$ converges.

(We also got the additional result that $\displaystyle \lVert e^A\rVert\leq e^{\lVert A\rVert} , \;\; \forall A \in E$ . )

They might interest you:

2 thoughts on “Exponential matrix”

Leave a Reply Cancel reply