Evaluate the product
![Rendered by QuickLaTeX.com \[\Pi = \prod_{k=1}^{n}\frac{(2k)^4+(2k)^2+1}{(2k-1)^4+(2k-1)^2+1}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-d47de6f97187884876e1fbbb27b2625c_l3.png)
Solution
We are making use of the identity
![]()
Hence,
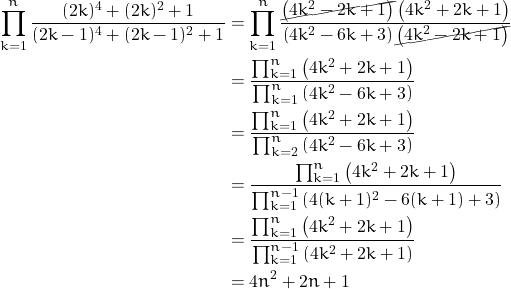
A site of university mathematics
Evaluate the product
![Rendered by QuickLaTeX.com \[\Pi = \prod_{k=1}^{n}\frac{(2k)^4+(2k)^2+1}{(2k-1)^4+(2k-1)^2+1}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-d47de6f97187884876e1fbbb27b2625c_l3.png)
Solution
We are making use of the identity
![]()
Hence,
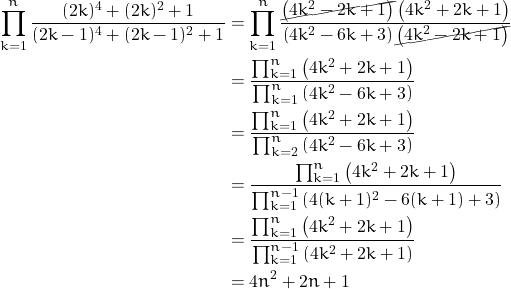
Prove that
![Rendered by QuickLaTeX.com \[\prod_{n=1}^{\infty} \left (1 + 2e^{-n \pi \sqrt{3}} \cosh \frac{n \pi}{\sqrt{3}} \right ) = \frac{\exp \left ( \frac{\pi \sqrt{3}}{18} \right )}{\sqrt[4]{3}}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-cdc9835bb5af97ed9fffbb794129579b_l3.png)
Solution
Let ![]() and
and ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \begin{align*} \prod_{n=1}^{\infty} \left (1 + 2e^{-n \pi \sqrt{3}} \cosh \frac{n \pi}{\sqrt{3}} \right ) &= \prod_{n=1}^{\infty} \left ( 1 + q + q^{2n} \right ) \\ &= \frac{\prod_{n=1}^{\infty} \left ( 1 - q^{3n} \right )}{\prod_{n=1}^{\infty} \left ( 1 - q^n \right )} \\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \frac{\eta(3\tau)}{\eta(\tau)} \\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \frac{\eta \left ( - 1/\tau \right )}{\eta(\tau)}\\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \sqrt{-i \tau} \\ &= frac{\exp \left ( \frac{\pi \sqrt{3}}{18} \right )}{\sqrt[4]{3}} \end{align*}](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-e72f41b960e6bdb7c06771a07cd9d377_l3.png)
Let ![]() denote the
denote the ![]() -th Fibonacci number and
-th Fibonacci number and ![]() the
the ![]() – th Lucas. Prove that
– th Lucas. Prove that
![]()
Solution
Exploiting the fact that ![]() we deduce that
we deduce that ![]() .
.
Lemma: Let ![]() be positive numbers. It holds that
be positive numbers. It holds that
![]()
Proof: Making use of Binet’s formula we have successively:

by cancellations and the fact that ![]() . This completes the proof of the lemma.
. This completes the proof of the lemma.
Setting ![]() we get the result.
we get the result.
Let ![]() denote the Fibonacci sequence. Prove that
denote the Fibonacci sequence. Prove that
![]()
Solution
Let ![]() denote the partial product. Thus,
denote the partial product. Thus,

Prove that
![]()
Solution
We simply note
![]()
and the result follows.